Manomagnetics with Mi_Magnet and Mi_µMagnet

Mi_Magnet and Mi_µMagnet are two codes, based on the classical Heisenberg model, that determine magnetic configurations by minimizing the energy.
They both make use of the fast multipole method (FMM) to compute efficiently the dipolar field (also called demagnetizing field). They are parallelized using MPI and OpenMP libraries and can thus be used to simulate systems with several millions of variables.
While Mi_Magnet (Jourdan et al., 2007) uses exclusively Heisenberg spins, Mi_µMagnet (Jourdan et al., 2008) also includes a micromagnetic description that is seamlessly coupled to the atomistic approach. The micromagnetic regions are described with an adaptive finite difference grid. They can be resolved at the atomic scale depending on the spatial variations of the magnetization or the presence of structural inhomogeneities.
Mi_µMagnet has been developed during the PhD thesis of Thomas JOURDAN.


Articles using Mi_Magnet or Mi_µMagnet



Jourdan T, Lançon F and Marty A
Multiscale method for Heisenberg spin simulations.
Physical Review B, 2008, 77: 224428
[article (pdf format)]
[copyright]



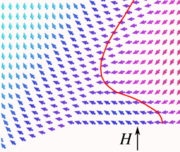Jourdan T, Lançon F and Marty A
Pinning of magnetic domain walls to structural defects in thin layers within a Heisenberg-type model.
Physical Review B, 2007, 75: 094422
[article (pdf format)]
[copyright APS]


Ernult F, Dieny B, Billard L, Lançon F and Regnard JR
Increase in ferromagnetic/antiferromagnetic exchange bias due to a reduction of the interfacial exchange interaction.
Journal of Applied Physics, 2003, 94: 6678-6682

Camarero J, Pennec Y, Vogel J, Bonfim M, Pizzini S, Ernult F, Fettar F, Garcia F, Lançon F, Billard L, Dieny B, Tagliaferri A and Brookes NB
Perpendicular interlayer coupling in Ni₈₀Fe₂₀/Co trilayers.
Physical Review Letters, 2003, 91: 027201/1-4


Contact
Mi_Magnet was originally developed by Frédéric Lançon and Luc Billard. The fast multipole method and Mi_µMagnet were coded by Thomas Jourdan as part of his PhD. For further information, please contact Frédéric Lançon or Thomas Jourdan.