In Bi₂Fe₄O₉, the Fe³⁺ ions form a magnetic Cairo pentagonal lattice. With the odd number of bonds per pentagon, the lattice is prone to geometric frustration, which results in a competition between spin pair interactions. It also has a complex connectivity with three- and four-fold connected Fe₁ and Fe₂ sites, contrary to the simpler triangle-based lattices. This results in an unconventional ground state consisting of an orthogonal arrangement of the magnetic moments below the ordering temperature TN ~ 240 K ^[1] (see figure 1a). This classical ground state was also obtained theoretically ^[2]. However, before our study, no experimental determination of the microscopic ingredients at the origin of this peculiar order had been reported.


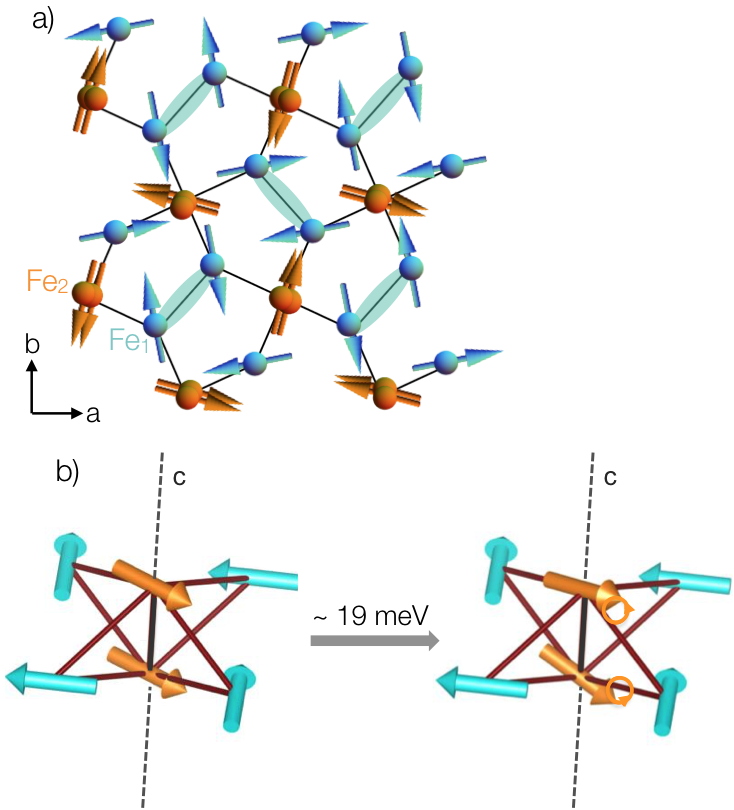Figure 1: Magnetic arrangement of the Fe₁ (in blue) and Fe₂ (in orange) on the pentagonal lattice. Blue ellipses underline strongly coupled antiferromagnetic Fe₁ spins (dimers). b) Schematic description of the local motion of two Fe₂ responsible for the flat mode observed at 19 meV in the inelastic spectrum.

In the present work, we present our measurements, using inelastic neutron scattering, of the rich excitation spectrum of Bi₂Fe₄O₉ reflecting the coexistence of local and collective motions of spins due to the complex geometry of the magnetic lattice.

On observe en effet une excitation non dispersive particulière située à une énergie constante pour tous les vecteurs de diffusion (voir figure 2c). Elle est liée à une précession locale d'une paire de spins Fe₂ qui ne se propage pas pour des raisons géométriques (voir figure 1b). En plus de ce mode, sont également visibles les ondes de spin dispersives attendues dans un tel système, résultant de la précession collective des moments magnétiques autour de leur position d'équilibre (représentées sur les figures 2a-c).

We indeed observe a peculiar nondispersive excitation located a constant energy for all scattering vectors (see figure 2c). It is related to a local precession of a pair of Fe₂ spins that do not propagate due to geometrical constrains (see figure 1b). In addition to this, expected dispersive spinwaves, arising from collective precession of the magnetic moments around their equilibrium position, are visible (shown in figures 2a-c). They allow us to determine quantitatively the complex magnetic interactions in Bi₂Fe₄O₉ from comparison with spin wave calculations (displayed in figures 2d-f). Five isotropic antiferromagnetic super-exchange interactions account for the magnetic order and for the associated excitations, including the peculiar flat mode. Strikingly, there is a hierarchy in the strength of these interactions that results in a lattice with dominant pairs of antiferromagnetically coupled spins Fe1 on almost orthogonal bonds (see figure 1a).


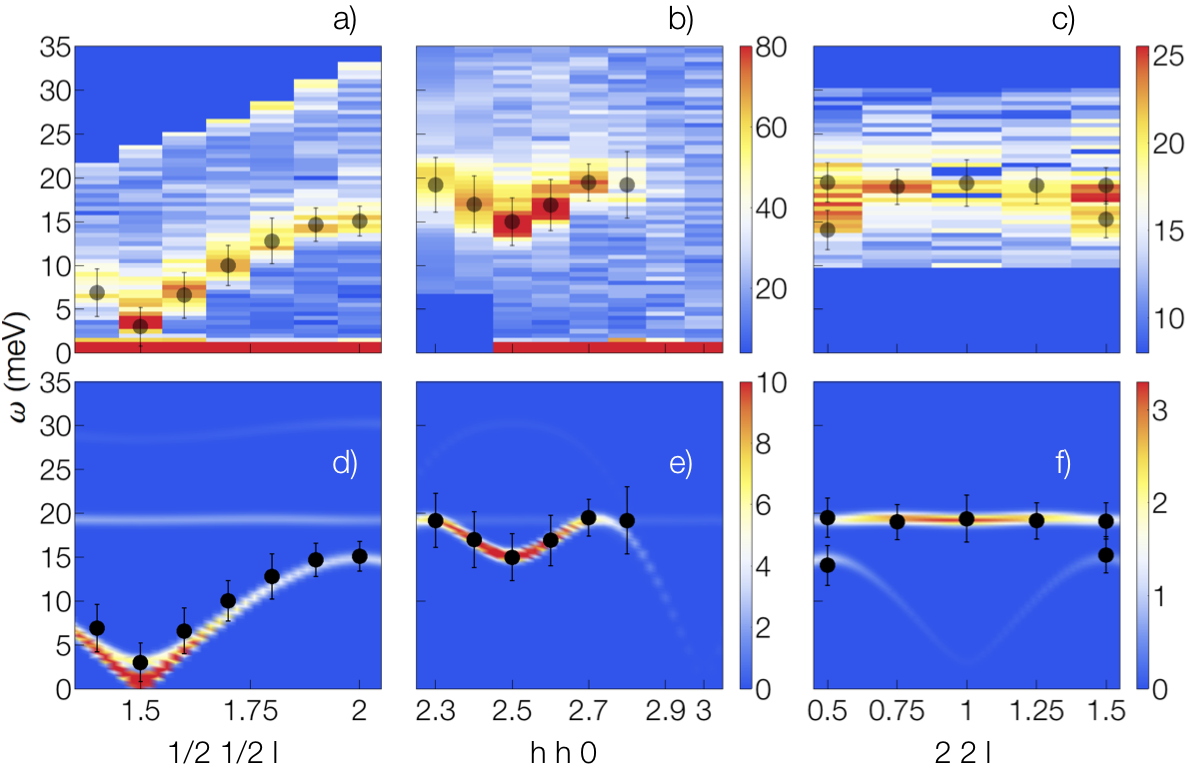Figure 2: Measured a–c) and calculated d–f) dynamic structure factor S(Q,ω).The black points on top of the measured and calculated) S(Q,ω) give the fitted energy positions of the experimental spin wave dispersion. The flat mode is present at the energy of 19 meV.

We investigated the fingerprint of these Fe₁ dimers in the paramagnetic state by measuring the magnetization distribution induced by a magnetic field above TN (see figure 3).


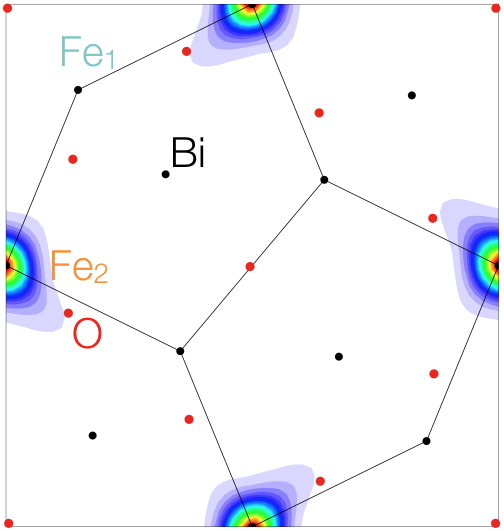Figure 3: Magnetization distribution projected along the c axis measured with polarized neutrons (flipping ratio method) under a magnetic field _µoH = 6 T applied along a - b at T = 250 K.

We found that the induced magnetization on site Fe₁ is vanishingly small whereas the Fe₂ ions carry a non negligible induced magnetic moment aligned along the field. This different response of both Fe types to the magnetic field confirms that, even at a temperature where the thermal fluctuations are expected to prevent magnetic ordering, strong antiferromagnetic correlations persist between the Fe₁ pairs. They form an array of dimers in a sea of fluctuating Fe₂ spins. Our study discloses, beyond the canonical examples of frustrated systems, novel behaviors that should be more generally observed in materials where the frustration is interlocked with complex connectivity and hierarchal interactions.